Préparation au Bac - Spécialité

Préparation au Bac 2023

Exercice 1 : Bac Spécialité 2023 (Métropole, septembre, jour 2) - Exercice 3 - Imprimante à jet d’encre continu

Imprimante à jet d’encre continu

De nombreuses applications technologiques, dans des domaines très variés, reposent sur l’utilisation d’un champ électrique.
L’objectif de cet exercice est d’étudier le principe de fonctionnement des imprimantes à jet d’encre continu dévié, principalement utilisées pour imprimer les dates d’expiration figurant sur les produits alimentaires.
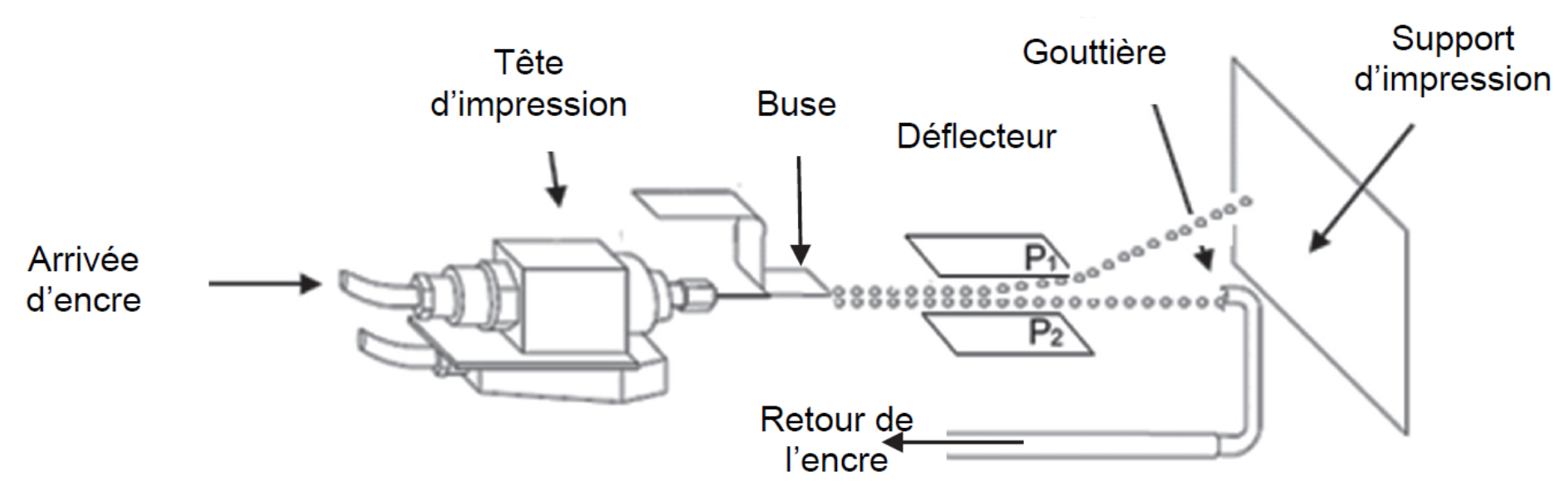
On donne sur le schéma de la figure 1, le principe de fonctionnement de l’imprimante à jet d’encre continu dévié : le jet d’encre sort de la tête d’impression par une buse qui le décompose en très petites gouttes dont certaines sont chargées électriquement.
Celles-ci passent sous un déflecteur constitué de deux plaques \(P1\) et \(P2\) parallèles, chargées électriquement, assimilables à un condensateur plan. Ces plaques dévient les gouttes chargées de leur trajectoire initiale.
Les gouttes non chargées poursuivent quant à elles leur mouvement rectiligne vers une gouttière de recyclage et sont réintégrées dans le module d’encre afin d’être réutilisées.

Schéma imprimante
Figure 1. Schéma de principe de l’imprimante à jet d’encre continu dévié (d’après le site timis.fr)

Données :

  • les mouvements sont étudiés dans le référentiel terrestre supposé galiléen associé au repère \((O, \vec{i}, \vec{k})\) représenté sur la figure 2. Les vecteurs \(\vec{i}\) et \(\vec{k}\) sont unitaires ;
  • on considère que la charge électrique et la masse des gouttes d’encre restent constantes entre la buse et le support d’impression ;
  • masse d’une goutte d’encre : \(m = 4×10^{-10}\: \text{kg} \) ;
  • charge électrique d’une goutte : \(q = -2×10^{-13}\:\text{C}\) ;
  • valeur de la vitesse d’éjection des gouttes d’encre : \(v_{0} = 20\:\text{m/s}\) ;
  • longueur des plaques du déflecteur : \(L = 3\:\text{cm}\) ;
  • distance entre le déflecteur et le support d’impression : \(D = 6\:\text{cm}\) ;
  • le champ électrique est supposé uniforme dans le déflecteur, il s’écrit \(\vec{E} = – E\vec{k}\) avec \(E = 8 \times 10^{5}\:\text{V}\mathord{\cdot}\text{m}^{-1}\) ;
  • le champ électrique est nul à l’extérieur du déflecteur ;
  • hauteur moyenne d’un caractère imprimé : \(h = 3\:\text{mm}\) ;
  • intensité de la pesanteur : \(g = 9,81\: \text{m}\cdot \text{s}^{-2}\).

On étudie le mouvement d’une goutte d’encre \(G\), supposée ponctuelle, de masse \(m\) et de charge \(q\) négative

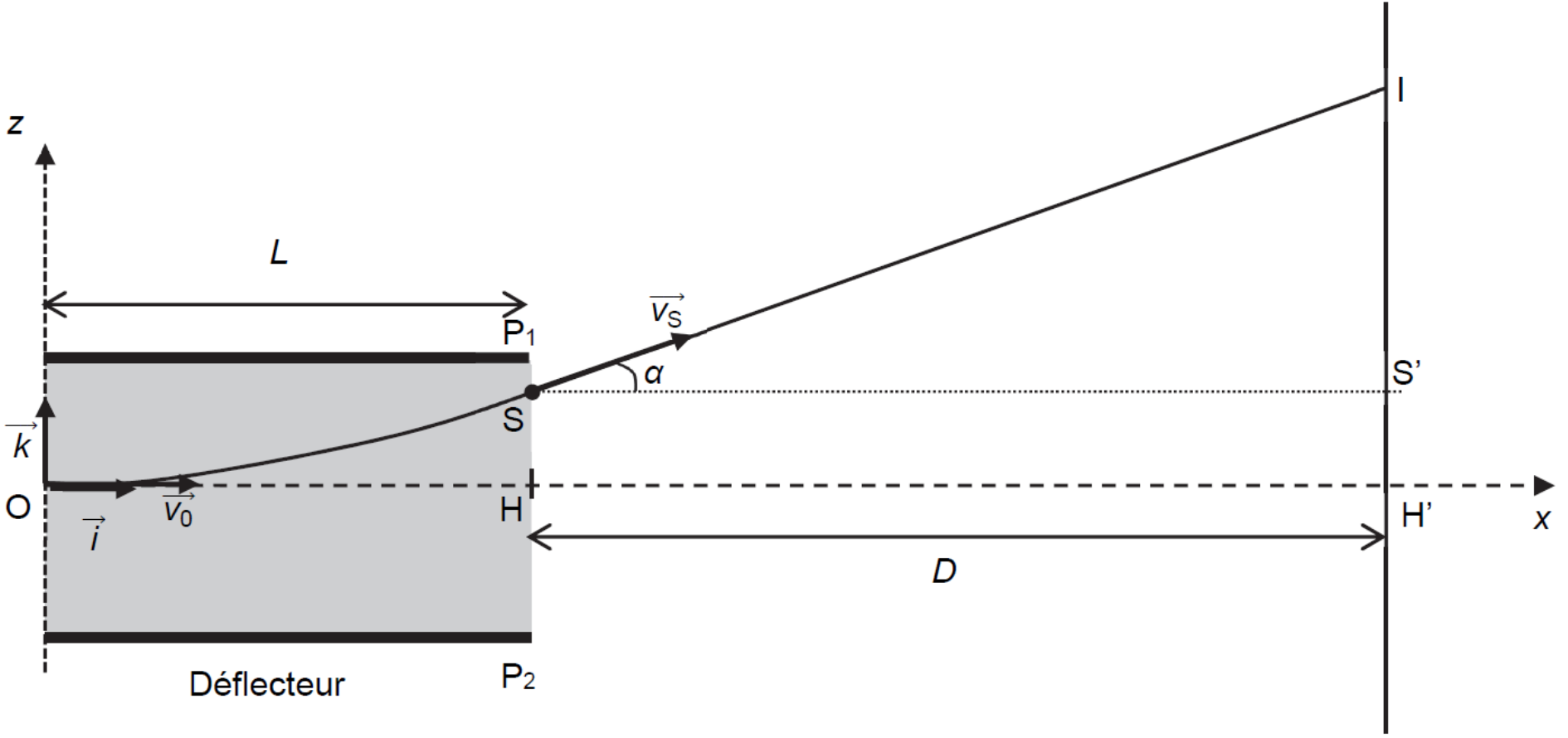
Graphique du mouvement du jet d'encre
Figure 2. Schéma de la trajectoire de la goutte \(G\)

À la date \(t_{0} = 0\:\text{s}\), la goutte d’encre \(G\) pénètre dans la zone de champ électrique uniforme au niveau du point \(O\) avec une vitesse initiale notée \(\vec{v_{0}} = v_{0} \vec{i} \).
On suppose que l’action mécanique de l’air est négligeable devant les autres actions.

1. a Indiquer les signes des charges portées par les plaques \(P1\) et \(P2\) sachant que la goutte chargée négativement est déviée vers le haut (sens des \(z\) croissants).
Le premier symbole correspondant à \(P1\) et le second à \(P2\).
1. b En déduire l’orientation du vecteur champ électrique \(\vec{E}\).

On suppose que la valeur du poids de la goutte d’encre \(G\) est négligeable par rapport à celle de la force électrique subie dans le déflecteur.
Établir l’expression du vecteur accélération \(\vec{a_{G}}\) de la goutte d’encre en fonction de la masse \(m\), de la charge \(q\) et du vecteur champ électrique \(\vec{E}\) entre les plaques du déflecteur.

2. a \(a_{Gx}(t)\) est égale à :
On donnera directement l’expression.
2. b \(a_{Gz}(t)\) est égale à :
On donnera directement l’expression.

Donner les expressions des équations horaires \(x_{G}(t)\) et \(z_{G}(t)\) du mouvement de la position de la goutte d’encre \(G\) dans le déflecteur.

3. a \(x_{G}(t)\) est égale à :
On donnera directement l’expression.
3. b \(z_{G}(t)\) est égale à
On donnera directement l’expression.
4. a Exprimer en fonction de \(L\) et \(v_{0}\) la date \(t_{S}\) à laquelle la goutte d’encre \(G\) sort du déflecteur.
On donnera directement l’expression.
4. b Calculer la valeur numérique de \(t_{S}\).
On donnera le résultat en s avec le nombre de chiffres significatifs permis par les données de l'énoncé.
4. c Calculer la valeur de la déviation \(HS\).
On donnera le résultat en mm avec le nombre de chiffres significatifs permis par les données de l'énoncé.

Donner les coordonnées du vecteur vitesse \(\vec{v_{S}}\) de la goutte d’encre \(G\) à la date \(t_{S}\).

5. a \(v_{x}(t_{s})\) est égale à :
On donnera le résultat en \(\text{m}/\text{s}\) avec le nombre de chiffres significatifs permis par les données de l'énoncé.
5. b \(v_{z}(t_{s})\) est égale à :
On donnera le résultat en \(\text{m}/\text{s}\) avec le nombre de chiffres significatifs permis par les données de l'énoncé.

On considère l’angle \(\alpha\) entre l’axe \((O_{x})\) et le vecteur vitesse \(\vec{v_{S}}\).

6 Déterminer l’expression de \(tan \alpha\) en fonction de \(q\), \(E\), \(L\), \(m\) et \(v_{0}\).
On donnera directement l’expression.

On suppose que le mouvement de la goutte entre le point \(S\) et le support d’impression est rectiligne uniforme.

7 En déduire la valeur de la hauteur \(H’I\) du point d’impact \(I\) de la goutte sur le support d’impression.
On donnera le résultat en \(mm\) avec le nombre de chiffres significatifs permis par les données de l'énoncé.
8. a Avec les données choisies, a-t-on imprimé un caractère de hauteur plus ou moins grande que la hauteur moyenne d’un caractère imprimé ?
8. b Cocher parmi les paramètres suivants celui ou ceux qui permettent d’augmenter la taille du caractère si on les augmente.

Exercice 2 : Bac Spécialité 2022 Mayotte Liban - Exercice 2 - QCM suites, fonctions et fonctions logarithmes

Un récipient contenant initialement \( 4 \) litres d’eau est laissé au soleil.
Toutes les heures, le volume d’eau diminue de \( 15 \) %.

Au bout de quel nombre entier d’heures le volume d’eau devient-il inférieur à un quart de litre ?

On considère la suite \( (u_{n}) \) définie pour tout entier naturel \( n \) par : \[ \left\{\begin{matrix} u_{n+1} = -5 + \dfrac{3}{2}u_n \\ u_{0} = -9 \end{matrix}\right. \]

On peut affirmer que :

On considère la fonction \( f \) définie sur l'intervalle \( ]0;+\infty[ \) par : \[ f(x) = 3ln(7x) \]

Pour tout réel \( x \) de l'intervalle \( ]0;+\infty[ \), on a :

On considère la fonction \( g \) définie sur l'intervalle \( ] \dfrac{1}{2};+\infty[ \) par : \[ g(x) = \dfrac{ln(2x)}{2x - 1} \]
On note \( C_g \) la courbe représentative de la fonction \( g \) dans un repère orthogonal.

La courbe \( C_g \) admet :

Dans la suite de l'exercice, on considère la fonction \( h \) définie sur l'intervalle \( ]0;2] \) par : \[ h(x) = 4x^{2}(1+2ln(x)) \]
On note \( C_h \) la courbe représentative de \( h \) dans un repère du plan.
On admet que \( h \) est deux fois dérivables sur l'intervalle \( ]0;2] \).
On note \( h' \) sa dérivée et \( h'' \) sa dérivée seconde.
On admet que, pour tout réel \( x \) de l'intervalle \( ]0;2] \), on a : \[ h'(x) = 16x(1+ln(x)) \]

Sur l'intervalle \( [\dfrac{1}{e};2] \), la fonction \( h \) s'annule :
Une équation de la tangente à \( C_h \) au point d'abscisse \( \sqrt{e} \) est :
Sur l'intervalle \( ]0;2] \), le nombre de points d'inflexion de la courbe \( C_h \) est égal à :

Exercice 3 : Bac Spécialité 2022 Amérique du Nord - Exercice 3 - Géométrie dans l’espace

Dans l’espace muni d’un repère orthonormé \((O; \overrightarrow{i}; \overrightarrow{j}; \overrightarrow{k})\) d’unité \(1 cm\), on considère les points suivants : \(J(0; 3; 3)\), \(K(-1; 5; 3)\), \(L(-4; 1; 0)\)

Donner la ou les caractéristiques correctes pour le triangle \(JKL\).
Donner une valeur approchée de l’aire du triangle \(JKL\).
On donnera le résultat en \(cm^{2}\) et arrondi à \(0,01 cm^{2}\) près.
Déterminer une valeur approchée au dixième de degré près de l’angle géométrique \(\widehat{JKL}\).
Sélectionner le ou les vecteurs normaux au plan \((JKL)\).
En déduire une équation cartésienne du plan \((JKL)\).

Dans la suite, \(T\) désigne le point de coordonnées \((3; 2; 1)\).

Lequel de ces systèmes d'équations paramétriques est une représentation paramétrique de la droite \( \Delta \), orthogonale au plan \(JKL\) et passant par \(T\) ?
Déterminer les coordonnées du point \(H\), projeté orthogonal du point \(T\) sur le plan \(JKL\).
On séparera les coordonnées avec un point-virgule.
Voici un exemple de réponse attendue : \((1;2;-1)\)

On rappelle que le volume \(V\) d’un tétraèdre est donné par la formule :

\(V = \frac{1}{3} B \times h\) où \(B\) désigne l’aire d’une base et \(h\) la hauteur correspondante.

Donner une valeur approchée du volume du tétraèdre \(JKLT\) en \(cm^{3}\).
On donnera le résultat arrondi à \(0,001cm^{3}\) près.

Exercice 4 : Bac 2023 (Amérique du Sud) – Exercice 1 : Étude de fonctions

Partie A

On considère la fonction \(f\) définie sur l'ensemble \([0; +\infty[ \) par \[f(x) = 3 + x^{2} -2x^{2}\operatorname{ln}\left(\dfrac{1}{2}x\right) \]
On admet que \(f\) est dérivable sur l'intervalle et on note \(f'\) sa fonction dérivée.

1. a Que vaut \( \lim_{x\to 0} x^{2}\operatorname{ln}\left(\dfrac{1}{2}x\right) \) ?
1. b En déduire \( \lim_{x\to 0} f(x) \).
1. c En remarquant que \( f(x) = 3 + x^{2}\left(1 -2\operatorname{ln}\left(\dfrac{1}{2}x\right)\right) \), déterminer \( \lim_{x\to + \infty} f(x)\).
2. Déterminer, pour tout réel \(x\) de l'intervalle \( ]0; +\infty[\), \(f'(x)\), l'expression de la fonction dérivée de \(f\).
On donnera directement \(f'(x)\)
3. Compléter le tableau de variations de \(f\) sur l'intervalle \(]0; + \infty[ \).

Essais restants : 2

4. Compléter la démonstration suivante montrant que l'équation \(f(x) = 0 \) admet une unique solution \(\alpha\) dans l'intervalle \([2; +\infty[\) et que \(\alpha \in [2; 2e]\)
La fonction \(f\) est continue car et \(f\) est sur l'intervalle \([2;+ \infty[\). 0 est compris entre \( f(2) = \) et \( \lim_{x\to + \infty} f(x) = \) . D'après le théorème , il existe un réel \(\alpha\), avec \(\alpha \in ]2;+\infty [ \) tel que \( f(\alpha) = \) . En appliquant le même théorème sur l'intervalle \([2;\) \(]\), on a bien compris entre \(f(2) = \) et \(f(2e) = 3 - 1e^{2} = \). D'où \( 1< \alpha < 2e\)

On admet dans la suite de l'exercice, que l'équation \( f(x) = 0 \) n'admet pas de solution sur l'intervalle \(]0;2]\).

5. On donne la fonction ci-dessous écrite en Python. L'instruction from lycee import * permet d'accèder à la fonction ln. 
from lycee import *

def f(x):
    return 3 + 1 * x ** 2 - 2 * x ** 2 * ln(1/2 * x)

def dichotomie(p):
    a = 2
    b = 2.7 / 0.5
    while b - a > 10 ** (-p):
        if f(a) * f((a + b) / 2) < 0:
            b = (a + b) / 2
        else:
            a = (a + b) / 2
    return (a, b)
On écrit dans la console d'exécution : 
>>> dichotomie(1)
Parmi les quatre propositions ci-dessous, déterminer celle affichée par l'instruction précédente.

Partie B

On considère la fonction \(g\) définie sur l'intervalle \(]0; +\infty[\), par \(g(x) = \dfrac{\operatorname{ln}\left(\dfrac{1}{2}x\right)}{3 + x^{2}}\) . On admet que \(g\) est dérivable sur l'intervalle \(]0; +\infty[\) et on note \(g'\) sa fonction dérivée. On note \(C_{g}\) la courbe représentative de la fonction \(g\) dans le plan rapporté à un repère \((O;\vec{i},\vec{j})\).

1. Déterminer, pour tout réel \(x\) de l'intervalle \(]0; +\infty[\), \(g'(x)\), l'expression de la fonction dérivée de \(g\).
2. Compléter la démonstration montrant que la fonction \(g\) admet un maximum en \(x = \alpha\).
\(g'\) peut être mise sous la forme \( \dfrac{f(x)}{x\left(3 + x^{2}\right)^{2}} \). Puisque \(x > 0 \) et \( (3 + x^{2})^2 \) \(0\), le signe de \(g'(x)\) est celui du numérateur donc le signe de . Or on a vu (Partie A question 3.) que \(f(x)\) \(0 \) sur \(]0;\alpha[ \) et \(f(x)\) \(0\) sur \(]\alpha; + \infty[ \). La fonction \(g\) est donc sur \([0; \alpha]\), puis sur \([\alpha; + \infty[\) avec un \(g(\alpha)\).

On admet que \(g(\alpha) = \)\(\dfrac{1}{2\alpha^2}\)

3. On note \(T_{2}\) la tangente à \(C_{g}\) au point d'abscisse 2 et on note \(T_{\alpha}\) la tangente à \(C_{g}\) au point d'abscisse \(\alpha\). Déterminer, en fonction de \(\alpha\), les coordonnées du point d'intersection des droites \(T_{2}\) et \(T_{\alpha}\).

Exercice 5 : Bac Spécialité 2021 Métropole - Exercice 1 - Probabilités

Dans une école de statistique, après étude des dossiers des candidats, le recrutement se fait de deux façons :

  • • \( 5 \)% des candidats sont sélectionnés sur dossier. Ces candidats doivent ensuite passer un oral à l’issue duquel \( 60 \)% d’entre eux sont finalement admis à l’école.
  • • Les candidats n’ayant pas été sélectionnés sur dossier passent une épreuve écrite à l’issue de laquelle \( 20 \) % d’entre eux sont admis à l’école.

Partie 1 : Arbre et calcul de probabilités

On choisit au hasard un candidat à ce concours de recrutement. On notera :

  • • \( D \) l’évènement « le candidat a été sélectionné sur dossier » ;
  • • \( A \) l’évènement « le candidat a été admis à l’école » ;
  • • \( \overline{D} \) et \( \overline{A} \) les évènements contraires des évènements \( D \) et \( A \) respectivement.
1. Compléter l'arbre ci-dessous :
On donnera les résultats arrondis au centième près.
{"D": {"A": {"value": " "}, "\\overline{A}": {"value": " "}, "value": " "}, "\\overline{D}": {"A": {"value": " "}, "\\overline{A}": {"value": " "}, "value": " "}}
2. Calculer la probabilité que le candidat soit sélectionné sur dossier et admis à l’école.
3. Calculer la probabilité de l'évènement \( A \).
4. On choisit au hasard un candidat admis à l’école. Quelle est la probabilité que son dossier n’ait pas été sélectionné ?
On arrondira le résultat au centième près.

Partie 2 : Variable aléatoire

Dans une autre école, la probabilité pour un candidat d’être admis à l’école est égale à \( 0,09 \). On considère un échantillon de dix-sept candidats choisis au hasard, en assimilant ce choix à un tirage au sort avec remise. On désigne par \( X \) la variable aléatoire dénombrant les candidats admis à l’école parmi les dix-sept tirés au sort. On admet que la variable aléatoire \( X \) suit une loi binomiale.

1. a. Quel est le paramètre \( n \) de cette loi ?
1. b Calculer la probabilité que trois des dix-sept candidats tirés au sort soient admis à l’école.
On donnera une réponse arrondie au centième.
1. c Calculer la probabilité qu’au moins un des dix-sept candidats tirés au sort soit admis à cette école.
On donnera une réponse arrondie au centième.

Un lycée présente \( n \) candidats au recrutement dans cette école, où \( n \) est un entier naturel non nul.
On admet que la probabilité pour un candidat quelconque du lycée d’être admis à l’école est égale à \( 0,09 \) et que les résultats des candidats sont indépendants les uns des autres.

2. a Donner l’expression, en fonction de \( n \), de la probabilité qu’aucun candidat issu de ce lycée ne soit admis à l’école.
2. b À partir de quelle valeur de l’entier \( n \) la probabilité qu’au moins un élève de ce lycée soit admis à l’école est-elle supérieure ou égale à \( 0,9 \) ?
Revenir au choix du niveau
False